Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Ваш комментарий о книге
Бирюков С., Чередов А. Метрология: Тексты лекций
4. Погрешности измерений
При практическом осуществлении процесса измерений независимо от точности средств измерений, правильности методики и тщательности
выполнения измерений результаты измерений отличаются от истинного значения измеряемой величины, т.е. неизбежны погрешности измерений. При оценке погрешности вместо истинного значения принимают действительное; следовательно, можно дать лишь приближенную оценку погрешности измерений. Оценка достоверности результата измерений, т.е. определение погрешности измерений - одна из основных задач метрологии [1].
Погрешность — это отклонение результата измерения от истинного значения измеряемой величины. Погрешности условно можно разделить на погрешности средств измерения и погрешности результата измерений.
Погрешности средств измерения были рассмотрены в главе 3.
Погрешность результата измерения — это число, указывающее возможные границы неопределенности значения измеряемой величины.
Ниже будет дана классификация и рассмотрены погрешности результата измерений.
По способу числового выражения различают абсолютные и относительные погрешности.
В зависимости от источника возникновения погрешности бывают инструментальные, методические, отсчитывания и установки.
По закономерностям проявления погрешности измерений делят на систематические, прогрессирующие, случайные и грубые.
Рассмотрим указанные погрешности измерений более подробно.
4.1. Абсолютные и относительные погрешности
Абсолютная погрешность D - это разность между измеренным X и истинным Xи значениями измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины: D = Х - Хи .
Поскольку истинное значение измеряемой величины определить невозможно, вместо него на практике используют действительное значение измеряемой величины Хд. Действительное значение находят экспериментально, путем применения достаточно точных методов и средств измерений. Оно мало отличается от истинного значения и для решения поставленной задачи может использоваться вместо него. При поверке за действительное значение обычно принимают показания образцовых средств измерений. Таким образом, на практике абсолютную погрешность находят по формуле D » Х – Хд . Относительная погрешность d — это отношение абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины (она обычно выражается в процентах) : 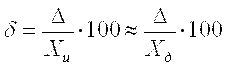 . .
4.2. Погрешности инструментальные и методические,
отсчитывания и установки
Инструментальными (приборными или аппаратурными) погрешностями называются такие, которые принадлежат данному средству измерений, могут быть определены при его испытаниях и занесены в его паспорт.
Эти погрешности обусловлены конструктивными и технологическими недостатками средств измерений, а также следствием их износа, старения или неисправности. Инструментальные погрешности, обусловленные погрешностями применяемых средств измерений, были рассмотрены в главе 3.
Однако, кроме инструментальных погрешностей, при измерениях возникают еще и такие погрешности, которые не могут быть приписаны данному прибору, не могут быть указаны в его паспорте и называются методическими, т.е. связанными не с самим прибором, а с методом его использования.
Методические погрешности могут возникать из-за несовершенства разработки теории явлений, положенных в основу метода измерений, неточности соотношений, используемых для нахождения оценки измеряемой величины, а также из-за несоответствия измеряемой величины и ее модели.
Рассмотрим примеры, иллюстрирующие методическую погрешность измерения.
Объектом исследования является источник переменного напряжения, амплитудное значение которого Um нужно измерить. На основании предварительного изучения объекта исследования за его модель принят генератор напряжения синусоидальной формы. Используя вольтметр, предназначенный для измерений действующих значений переменных напряжений, и зная соотношение между действующим и амплитудным значениями синусоидального напряжения, получаем результат измерения в виде Um =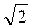 ×Uv, где Uv - показание вольтметра. Более тщательное изучение объекта могло бы выявить, что форма измеряемого напряжения отличается от синусоидальной и более правильное соотношение между значением измеряемой величины и показанием вольтметра Um =k×Uv , где k ¹ ×Uv, где Uv - показание вольтметра. Более тщательное изучение объекта могло бы выявить, что форма измеряемого напряжения отличается от синусоидальной и более правильное соотношение между значением измеряемой величины и показанием вольтметра Um =k×Uv , где k ¹ 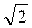 . Таким образом, несовершенство принятой модели объекта исследования приводит к методической погрешности измерения DU = . Таким образом, несовершенство принятой модели объекта исследования приводит к методической погрешности измерения DU = 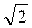 ×Uv - k×Uv . ×Uv - k×Uv .
Эту погрешность можно уменьшить, либо рассчитав значение k на основе анализа формы кривой измеряемого напряжения, либо заменив средство измерений, взяв вольтметр, предназначенный для измерений амплитудных значений переменных напряжений [11].
Очень часто встречающейся причиной возникновения методических погрешностей является то обстоятельство, что, организуя измерения, мы вынуждены измерять (или сознательно измеряем) не ту величину, которая должна быть измерена, а некоторую другую, близкую, но не равную ей [6].
Примером такой методической погрешности может служить погрешность измерения напряжения вольтметром с конечным сопротивлением (рис. 4.1).
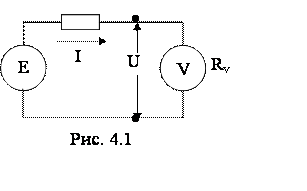 Вследствие шунтирования вольтмет-ром того участка цепи, на котором измеряется напряжение, оно оказывается меньшим, чем было до присоединения вольтметра. И действительно, напряжение, которое покажет вольтметр определится выражением U = I×Rv. Если учесть, что ток в цепи I = E/(Ri + Rv), то Вследствие шунтирования вольтмет-ром того участка цепи, на котором измеряется напряжение, оно оказывается меньшим, чем было до присоединения вольтметра. И действительно, напряжение, которое покажет вольтметр определится выражением U = I×Rv. Если учесть, что ток в цепи I = E/(Ri + Rv), то
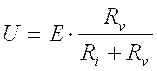 < < 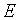 . .
Поэтому для одного и того же вольтметра, присоединяемого поочередно к разным участкам исследуемой цепи, эта погрешность различна: на низкоомных участках она ничтожна, а на высокоомных может быть очень большой. Эта погрешность могла бы быть устранена, если бы вольтметр был постоянно подключен к данному участку цепи на все время работы устройства (как на щите электростанции), но это невыгодно по многим причинам.
Нередки случаи, когда вообще трудно указать способ измерения, исключающий методическую погрешность. Пусть, например, измерению подлежит температура раскаленных болванок, поступающих из печи на прокатный стан. Спрашивается, где разместить датчик температуры (например, термопару): под болванкой, сбоку или над болванкой? Где бы мы его ни поместили, мы не измерим внутренней температуры тела болванки, т.е. будем иметь существенную методическую погрешность, так как измеряем не то, что нужно, а то, что проще (не сверлить же в каждой болванке канал, чтобы поместить термопару в её центре).
Таким образом, основной отличительной особенностью методических погрешностей является то обстоятельство, что они не могут быть указаны в паспорте прибора, а должны оцениваться самим экспериментатором при организации выбранной методики измерений, поэтому он обязан четко различать фактически измеряемую им величину от подлежащей измерению.
Погрешность отсчитывания происходит от недостаточно точного отсчитывания показаний. Она обусловлена субъективными особенностями наблюдателя (например, погрешность интерполирования, т.е. неточного отсчета долей деления по шкале прибора) и вида отсчетного устройства (например, погрешность от параллакса). Погрешности отсчитывания отсутствуют при использовании цифровых измерительных приборов, что является одной из причин перспективности последних.
Погрешность установки вызывается отклонением условий измерения от нормальных, т.е. условий, при которых производилась градуировка и поверка средств измерений. Сюда относится, например, погрешность от неправильной установки прибора в пространстве или его указателя на нулевую отметку, от изменения температуры, напряжения питания и других влияющих величин.
Рассмотренные виды погрешностей в равной степени пригодны для характеристики точности как отдельных результатов измерений, так и средств измерений.
4.3. Систематические, прогрессирующие, случайные и грубые погрешности
Систематическая погрешность измерений Dс — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины [2, 3].
Причины возникновения систематических погрешностей обычно могут быть установлены при подготовке и проведении измерений. Эти причины весьма разнообразны: несовершенство используемых средств и методов измерений, неправильная установка средства измерений, влияние внешних факторов (влияющих величин) на параметры средств измерений и на сам объект измерения, недостатки метода измерения (методические погрешности), индивидуальные особенности оператора (субъективные погрешности) и др. [7]. По характеру проявления систематические погрешности делятся на постоянные и переменные. К постоянным относятся, например, погрешности, обусловленные неточностью подгонки значения меры, неправильной градуировкой шкалы прибора, неправильной установкой прибора относительно направления магнитных полей и т.д. Переменные систематические погрешности обусловлены воздействием на процесс измерения влияющих величин и могут возникнуть, например, при изменении напряжения источника питания прибора, внешних магнитных полей, частоты измеряемого переменного напряжения и пр. Основная особенность систематических погрешностей состоит в том, что зависимость их от влияющих величин подчиняется определенному закону. Этот закон может быть изучен, а результат измерения - уточнен путем внесения поправок, если числовые значения этих погрешностей определены. Другим способом уменьшения влияния систематический погрешностей является применение таких методов измерения, которые дают возможность исключить влияние систематических погрешностей без определения их значений (например, метод замещения).
Результат измерений тем ближе к истинному значению измеряемой величины, чем меньше оставшиеся неисключенные систематические погрешности. Наличие исключенных систематических погрешностей определяет правильность измерений, качество, отражающее близость к нулю систематических погрешностей [2, 7]. Результат измерения будет настолько правильным, насколько он неискажен систематическими погрешностями и тем правильнее, чем меньше эти погрешности.
Прогрессирующими (или дрейфовыми) называются непредсказуемые погрешности, медленно изменяющиеся во времени. Эти погрешности, как правило, вызываются процессами старения тех или иных деталей аппаратуры (разрядка источников питания, старение резисторов, конденсаторов, деформация механических деталей, усадка бумажной ленты в самопишущих приборах и т. п.). Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы путем введения поправки лишь в заданный момент времени, а далее вновь непредсказуемо возрастают. Поэтому в отличие от систематических погрешностей, которые могут быть скорректированы поправкой, найденной один раз на весь срок службы прибора, прогрессирующие погрешности требуют непрерывного повторения коррекции и тем чаще, чем меньше должно быть их остаточное значение. Другая особенность прогрессирующих погрешностей состоит в том, что их изменение во времени представляет собой нестационарный случайный процесс и поэтому в рамках хорошо разработанной теории стационарных случайных процессов они могут быть описаны лишь с оговорками.
Случайная погрешность измерения 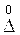 — составляющая погрешности измерений, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Значение и знак случайных погрешностей определить невозможно, они не поддаются непосредственному учету вследствие их хаотического изменения, обусловленного одновременным воздействием на результат измерения различных независимых друг от друга факторов. Обнаруживаются случайные погрешности при многократных измерениях одной и той же величины (отдельные измерения в этом случае называются наблюдением) одними и теми же средствами измерения в одинаковых условиях одним и тем же наблюдателем, т.е. при равноточных (равнорассеянных) измерениях. Влияние случайных погрешностей на результат измерения учитывается методами математической статистики и теории вероятности. — составляющая погрешности измерений, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Значение и знак случайных погрешностей определить невозможно, они не поддаются непосредственному учету вследствие их хаотического изменения, обусловленного одновременным воздействием на результат измерения различных независимых друг от друга факторов. Обнаруживаются случайные погрешности при многократных измерениях одной и той же величины (отдельные измерения в этом случае называются наблюдением) одними и теми же средствами измерения в одинаковых условиях одним и тем же наблюдателем, т.е. при равноточных (равнорассеянных) измерениях. Влияние случайных погрешностей на результат измерения учитывается методами математической статистики и теории вероятности.
Грубые погрешности измерений - случайные погрешности измерений, существенно превышающие ожидаемые при данных условиях погрешности.
Грубые погрешности (промахи) обычно обусловлены неправильным отсчетом по прибору, ошибкой при записи наблюдений, наличием сильно влияющей величины, неисправностью средств измерений и другими причинами. Как правило, результаты измерений, содержащие грубые погрешности, не принимаются во внимание, поэтому грубые погрешности мало влияют на точность измерения. Обнаружить промах бывает не всегда легко, особенно при единичном измерении; часто трудно бывает отличить грубую погрешность от большой по значению случайной погрешности. Если грубые погрешности встречаются часто, мы поставим под сомнение все результаты измерений. Поэтому грубые погрешности влияют на годность измерений.
В заключение описанного деления погрешностей средств и результатов измерений на случайную, прогрессирующую и систематическую составляющие необходимо обратить внимание на то, что такое деление является весьма упрощенным приемом их анализа. Поэтому всегда следует помнить, что в реальной действительности эти составляющие погрешности проявляются совместно и образуют единый нестационарный случайный процесс. Погрешность результата измерений при этом можно представить в виде суммы случайных 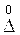 и систематических Dс погрешностей: D = Dс + и систематических Dс погрешностей: D = Dс +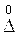 . В погрешности измерений входит случайная составляющая, поэтому её следует считать случайной величиной. . В погрешности измерений входит случайная составляющая, поэтому её следует считать случайной величиной.
Рассмотрение характера проявления погрешностей измерений показывает, нам, что единственно правильный путь оценки погрешностей дает нам теория вероятностей и математическая статистика.
4.4. Вероятностный подход к описанию погрешностей
Законы распределения случайных погрешностей. Случайные погрешности обнаруживают при проведении ряда измерений одной и той же величины. Результаты измерений при этом, как правило, не совпадают между собой, так как из-за суммарного воздействия множества различных факторов, не поддающихся учету, каждое новое измерение дает и новое случайное значение измеряемой величины. При правильном проведении измерений, достаточном их числе и исключении систематических погрешностей и промахов можно утверждать, что истинное значение измеряемой величины не выходит за пределы значений, полученных при этих измерениях. Оно остается неизвестным до тех пор пока не определено теоретически вероятное значение случайной погрешности.
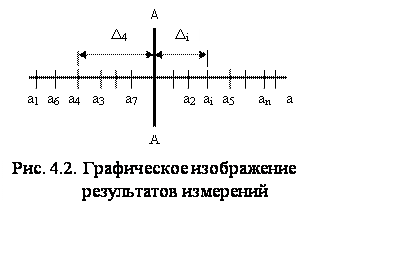
Пусть величину А измеряли п раз и наблюдали при этом значения а1, a2, а3,…,аi,...,аn. Случайная абсолютная погрешность единичного измерения определяется разностью
Di = ai – A . (4.1)
Графически результаты отдельных измерений представлены на рис. 4.2.
При достаточно большом числе п одни и те же погрешности, если они имеют ряд дискретных значений, повторяются и поэтому можно установить относительную частоту (частость) их появления, т.е. отношение числа полученных одинаковых данных mi к общему числу проведенных измерении п. При продолжении измерений величины А эта частота не изменится, поэтому ее можно считать вероятностью появления погрешности при данных измерениях: p(Ai) = mi / n.
 Статистическая зависимость вероятности появления случайных погрешностей от их значения называется законом распределе- ния погрешностей или законом распределения вероятности. Этот закон определяет характер появления различных результатов отдельных измерений. Различают два вида описания законов распределения: интегральный и дифференциальный. Статистическая зависимость вероятности появления случайных погрешностей от их значения называется законом распределе- ния погрешностей или законом распределения вероятности. Этот закон определяет характер появления различных результатов отдельных измерений. Различают два вида описания законов распределения: интегральный и дифференциальный.
Интегральным законом, или функцией распределения вероятностей F(D) случайной погрешности Di в i-м опыте, называют функцию, значение которой для каждого Dявляется вероятностью события Р(D), заключающегося в том, что случайная погрешность Diпринимает значения, меньше некоторого значения D, т.е. функцию F(D) = Р[Di < D]. Эта функция при изменении Dот -¥ до +¥ принимает значения от 0 до 1 и является неубывающей. Она существует для всех случайных величин как дискретных, так и непрерывных (рис 4.3 а).
Если F(D) симметрична относительно точки А, соответствующей вероятности 0,5 , то распределение результатов наблюдения будет симметрично относительно истинного значения А. В этом случае целесообразно F(D) сдвинуть по оси абсцисс на значение DA, т.е. исключить систематическую составляющую погрешность (DА = Dс) и получить функцию распределения случайной составляющей погрешности D = 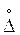 (рис. 4.3 б). Функция распределения вероятности погрешности D отличается от функции распределения вероятности случайной составляющей погрешности только сдвигом по оси абсцисс на значение систематической составляющей погрешности Dс . (рис. 4.3 б). Функция распределения вероятности погрешности D отличается от функции распределения вероятности случайной составляющей погрешности только сдвигом по оси абсцисс на значение систематической составляющей погрешности Dс .
Дифференциальным законом распределения вероятностей для случайной погрешности с непрерывной и дифференцируемой функцией распределения F(D) называют функцию 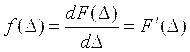 . Эта зависимость есть плотность распределения вероятностей. График плотности распределения вероятностей может иметь различную форму в зависимости от закона распределения погрешностей. Для F(D), изображенной на рис. 4.3 б, кривая распределения f(D) имеет форму, близкую к форме колокола (рис. 4.3 в). . Эта зависимость есть плотность распределения вероятностей. График плотности распределения вероятностей может иметь различную форму в зависимости от закона распределения погрешностей. Для F(D), изображенной на рис. 4.3 б, кривая распределения f(D) имеет форму, близкую к форме колокола (рис. 4.3 в).
Вероятность появления случайных погрешностей определяется площадью, ограниченной кривой f(D) или её частью и осью абсцисс (рис. 4.3 в). В зависи мости от рассматриваемого интервала погрешности 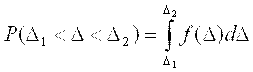 . .
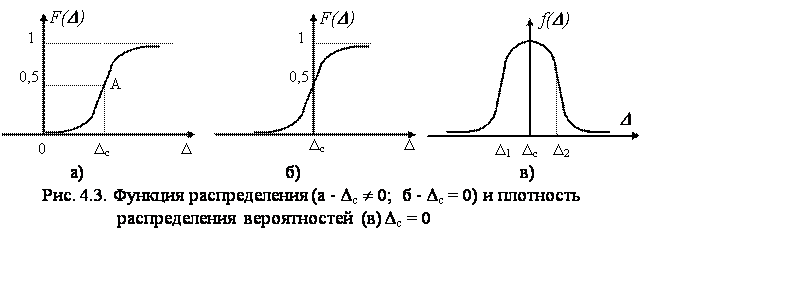
Значение f(D)dD есть элемент вероятности, равный площади прямоугольника с основанием dD и абсциссами D1 , D2, называемыми квантилями. Так как F(+¥)=1, то справедливо равенство 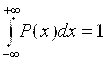 , ,
т.е. площадь под кривой f(D) согласно правилу нормирования равна единице и отражает вероятность всех возможных событий.
В практике электрических измерений одним из наиболее распространенных законов распределения случайных погрешностей является нормальный закон (Гаусса).
Математическое выражение нормального закона имеет вид
 , ,
где f(D) – плотность вероятности случайной погрешности D = аi - A; s - среднее квадратическое отклонение. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдений Di (см. формулу (4.1)):
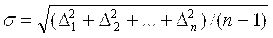 . .
Характер кривых, описанных этим уравнением для двух значений s, показан на рис. 4.4. Из этих кривых видно, что чем меньше s, тем чаще встречаются малые случайные погрешности, т.е. тем точнее выполнены измерения. В практике измерений встречаются и другие законы распределения, которые могут быть установлены на основании статистической обработки
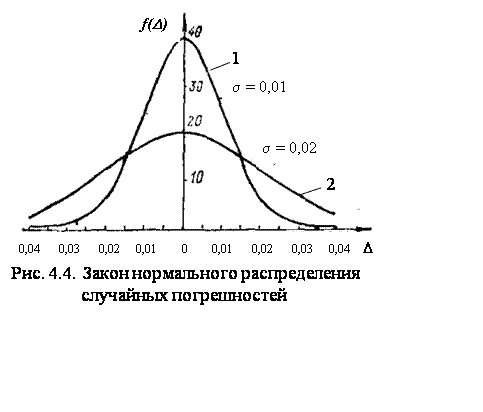 опытных данных. Некоторые из наиболее часто встречающихся законов распределения приведены в ГОСТ 8.011-84 «Показатели точности измерений и формы представления результатов измерений». опытных данных. Некоторые из наиболее часто встречающихся законов распределения приведены в ГОСТ 8.011-84 «Показатели точности измерений и формы представления результатов измерений».
Основными характеристи- ками законов распределения являются математическое ожидание и дисперсия.
Математическое ожидание случайной величины - это такое ее значение, вокруг которого группируются результаты отдельных наблюдений. Мате-матическое ожидание дискрет-ной случайной величины М[X] определяется как сумма произ-ведений всех возможных значений случайной величины на вероятность этих значений  . .
Для непрерывных случайных величин приходится прибегать к интегрированию, для чего необходимо знать зависимость плотности вероятности от х , т. е. f(х), где х=D. Тогда 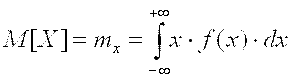 . .
Это выражение означает, что математическое ожидание равно сумме бесконечно большого числа произведений всех возможных значений случайной величины х на бесконечно малые площади f(х)dх, где f(х) —ординаты для каждого х, a dх - элементарные отрезки оси абсцисс.
Если наблюдается нормальное распределение случайных погрешностей, то математическое ожидание случайной погрешности равно нулю (рис. 4.4). Если же рассматривать нормальное распределение результатов, то математическое ожидание будет соответствовать истинному значению измеряемой величины, которое мы обозначаем через A.
Систематическая погрешность при этом представляет собой отклонение математического ожидания результатов наблюдений от истинного значения А измеряемой величины: Dс = М[X] – A, а случайная погрешность – разность между результатом единичного наблюдения и математическим ожиданием: 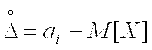 . .
Дисперсия ряда наблюдений характеризует степень рассеивания (разброса) результатов отдельных наблюдений вокруг математического ожидания:
D[X] =Dx=M[(ai – mx)2].
Чем меньше дисперсия, тем меньше разброс отдельных результатов, тем точнее выполнены измерения. Однако дисперсия выражается в единицах в квадрате измеряемой величины. Поэтому в качестве характеристики точности ряда наблюдений наиболее часто применяют среднее квадратическое отклонение (СКО), равное корню квадратному из дисперсии : 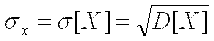 . .
Рассмотренное нормальное распределение случайных величин, в том числе и случайных погрешностей, является теоретическим, поэтому описанное нормальное распределение следует рассматривать как «идеальное», т. е. как теоретическую основу для изучения случайных погрешностей и их влияния на результат измерений.
Далее излагаются способы применения этого распределения на практике с той или иной степенью приближения. Рассматривается также еще одно распределение (распределение Стьюдента), применяемое при небольших количествах наблюдений.
Оценки погрешностей результатов прямых измерений. Пусть было проведено п прямых измерений одной и той же величины. В общем случае в каждом из актов измерений погрешность будет разной:
Di = ai – A,
где Di - погрешность i-го измерения; ai - результат i-го измерения.
Поскольку истинное значение измеряемой величины A неизвестно, непосредственно случайную абсолютную погрешность вычислить нельзя. При практических расчетах приходится вместо A использовать его оценку. Обычно принимают, что истинное значение равно среднему арифметическому значению ряда измерений:
 . (4.2) . (4.2)
где аi - результаты отдельных измерений; п — число измерений.
Теперь аналогично выражению (4.1) можно определить отклонение результата каждого измерения от среднего значения 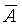 : :
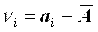 (4.3) (4.3)
где vi - отклонение результата единичного измерения от среднего значения. Следует помнить, что сумма отклонений результата измерений от среднего значения равна нулю, а сумма их квадратов минимальна, т. е.
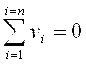 и и  min. min.
Эти свойства используются при обработке результатов измерений для контроля правильности вычислений.
Затем вычисляют оценку значения средней квадратической погрешности для данного ряда измерений
 . (4.4) . (4.4)
Согласно теории вероятностей при достаточно большом числе измерений, имеющих независимые случайные погрешности, оценка S сходится по вероятности к s. Таким образом,
 . (4.5) . (4.5)
Ввиду того что среднее арифметическое значение 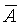 также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения. Эту величину обозначим символом sср. Можно показать, что для независимых погрешностей также является случайной величиной, имеет смысл понятие среднеквадратического отклонения среднего арифметического значения. Эту величину обозначим символом sср. Можно показать, что для независимых погрешностей
 . (4.6) . (4.6)
Значение sср характеризует степень разброса 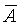 . Как указывалось выше, . Как указывалось выше, 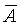 выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому sср называют также средней квадратической погрешностью результата измерений. выступает оценкой истинного значения измеряемой величины, т.е. является конечным результатом выполняемых измерений. Поэтому sср называют также средней квадратической погрешностью результата измерений.
На практике значением s, вычисляемым по формуле (4.5), пользуются в том случае, если необходимо дать характеристику точности применяемого метода измерения: если метод точен, то разброс результатов отдельных измерений мал, т.е. мало значение s. Значение же sср , вычисляемое по (4.6), используется для характеристики точности результата измерений некоторой величины, т.е. результата, полученного посредством математической обработки итогов целого ряда отдельных прямых измерений.
При оценке результатов измерений иногда пользуются понятием максимальной или предельной допустимой погрешности, значение которой определяют в долях s или S . В настоящее время существуют разные критерии установления максимальной погрешности, т. е. границы поля допуска ±D, в которые случайные погрешности должны уложиться. Общепринятым пока является определение максимальной погрешности D = 3s (или 3S). В последнее время на основании информационной теории измерений профессор П. В. Новицкий рекомендует пользоваться значением D = 2s.
Введем теперь важные понятия доверительной вероятности и доверительного интервала. Как указывалось выше, среднее арифметическое значение 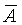 , полученное в результате некоторого ряда измерений, является оценкой истинного значения А и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что , полученное в результате некоторого ряда измерений, является оценкой истинного значения А и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Рд есть вероятность того, что 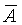 отличается от А не более чем на D, т.е. Р( отличается от А не более чем на D, т.е. Р(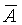 -D< А< -D< А<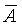 +D)=Рд . Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от +D)=Рд . Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины от 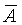 -D до -D до 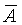 +D - доверительным интервалом. +D - доверительным интервалом.
Приведенные выше неравенства означают, что с вероятностью Рд доверительный интервал от 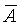 -D до -D до 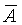 +D заключает в себе истинное значение А. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (п < 20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших п, но значительно отличающуюся от нормальной при малых п. +D заключает в себе истинное значение А. Таким образом, чтобы характеризовать случайную погрешность достаточно полно, надо располагать двумя числами — доверительной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал. В частности, при достаточно большом числе измерений часто бывает оправданным использование нормального закона, в то время как при небольшом числе измерений (п < 20), результаты которых принадлежат нормальному распределению, следует пользоваться распределением Стьюдента. Это распределение имеет плотность вероятностей, практически совпадающую с нормальной при больших п, но значительно отличающуюся от нормальной при малых п.
В табл. 4.1 приведены так называемые квантили распределения Стьюдента ½t(n)½Рд для числа измерений п = 2 - 20 и доверительных вероятностей Р = 0,5 - 0,999.
Укажем, однако, что обычно таблицы распределения Стьюдента приводятся не для значений п и Рд , а для значений m = n-1 иa =1 – Рд , что следует учитывать при пользовании ими. Чтобы определить доверительный интервал, надо для данных п и Рд найти квантиль ½t(n)½Рд и вычислить величины Ан = 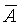 - sср× ½t(n)½Рд и Ав = - sср× ½t(n)½Рд и Ав = 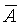 + sср× ½t(n)½Рд, которые будут являться нижней и верхней границами доверительного интервала. + sср× ½t(n)½Рд, которые будут являться нижней и верхней границами доверительного интервала.
После нахождения доверительных интервалов для заданной доверительной вероятности согласно выше приведенной методике делают запись результата измерения в виде 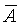 ; D = Dн ¸ Dв ; Рд , ; D = Dн ¸ Dв ; Рд ,
где 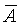 - оценка истинного значения результата измерения в единицах измеряемой величины; D - погрешность измерения; Dв = +sср× ½t(n)½Рд и Dн = -sср× ½t(n)½Рд – верхняя и нижняя границы погрешности измерения; Рд – доверительная вероятность [14]. - оценка истинного значения результата измерения в единицах измеряемой величины; D - погрешность измерения; Dв = +sср× ½t(n)½Рд и Dн = -sср× ½t(n)½Рд – верхняя и нижняя границы погрешности измерения; Рд – доверительная вероятность [14].
Таблица 4.1
n |
Значения квантилей распределения Стьюдента t(n) при доверительной
вероятности Рд |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0.99 |
0,995 |
0,999 |
2 |
1.000 |
1.376 |
1,963 |
3,080 |
6,310 |
12,71 |
31,80 |
63,70 |
127,3 |
637,2 |
3 |
0.816 |
1,061 |
1,336 |
1,886 |
2,920 |
4,30 |
6,96 |
9,92 |
14,10 |
31,60 |
4 |
0.765 |
0.978 |
1,250 |
1,638 |
2,350 |
3,18 |
4,54 |
5,84 |
7,50 |
12,94 |
5 |
0.741 |
0.941 |
1,190 |
1,533 |
2,130 |
2,77 |
3,75 |
4,60 |
5,60 |
8,61 |
6 |
0,727 |
0.920 |
1,156 |
1,476 |
2,020 |
2,57 |
3,36 |
4,03 |
4,77 |
6,86 |
7 |
0,718 |
0.906 |
1,134 |
1,440 |
1,943 |
2,45 |
3,14 |
3,71 |
4,32 |
5,96 |
8 |
0.711 |
0.896 |
1,119 |
1,415 |
1,895 |
2,36 |
3,00 |
3,50 |
4,03 |
5,40 |
9 |
0.706 |
0.889 |
1,108 |
1,397 |
1,860 |
2,31 |
2,90 |
3,36 |
3,83 |
5,04 |
10 |
0,703 |
0.883 |
1,110 |
1,383 |
1,833 |
2,26 |
2,82 |
3,25 |
3,69 |
4,78 |
11 |
0.700 |
0.879 |
1,093 |
1,372 |
1,812 |
2,23 |
2,76 |
3,17 |
3,58 |
4,59 |
12 |
0.697 |
0.876 |
1,088 |
1.363 |
1,796 |
2,20 |
2,72 |
3,11 |
3,50 |
4,49 |
13 |
0.695 |
0.873 |
1,083 |
1,356 |
1,782 |
2,18 |
2,68 |
3,06 |
3,43 |
4,32 |
14 |
0.694 |
0.870 |
1,079 |
1,350 |
1,771 |
2,16 |
2,65 |
3,01 |
3,37 |
4,22 |
15 |
0.692 |
0,868 |
1,076 |
1,345 |
1,761 |
2,14 |
2,62 |
2,98 |
3,33 |
4,14 |
16 |
0.691 |
0,866 |
1,074 |
1,341 |
1,753 |
2,13 |
2,60 |
2,95 |
3,29 |
4,07 |
17 |
0.690 |
0.865 |
1,071 |
1,337 |
1,746 |
2,12 |
2,58 |
2,02 |
3,25 |
4,02 |
18 |
0,689 |
0.863 |
1,069 |
1,333 |
1,740 |
2,11 |
2,57 |
2,90 |
3,22 |
3,96 |
19 |
0.688 |
0,862 |
1,067 |
1,330 |
1,734 |
2,10 |
2,55 |
2,88 |
3,20 |
3,92 |
20 |
0.688 |
0.861 |
1,066 |
1,328 |
1,729 |
2,09 |
2,54 |
2,86 |
3,17 |
3,88 |
¥ |
0,674 |
0,842 |
1,036 |
1,282 |
1,645 |
1,96 |
2,33 |
2,58 |
2,81 |
3,29 |
Оценка погрешностей результатов косвенных измерений. При косвенных измерениях искомая величина А функционально связана с одной или несколькими непосредственно измеряемыми величинами: х, y,...,t. Рассмотрим простейший случай определения погрешности при одной переменной, когда A=F(x). Обозначив абсолютную погрешность измерения величины х через ±Dx , получим A+DA= F(x±Dx).
Разложив правую часть этого равенства в ряд Тейлора и пренебрегая членами разложения, содержащими Dх в степени выше первой, получим
A+DA » F(x) ± 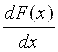 Dx или DA » ± Dx или DA » ± 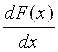 Dx. Dx.
Относительная ошибка измерения функции определится из выражения
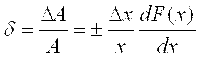 . .
Если измеряемая величина А является функцией нескольких переменных: A=F(x, y,...,t), то абсолютная погрешность результата косвенных измерений
 . .
Частные относительные погрешности косвенного измерения определяются по формулам 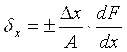 ; ; 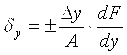 и т. д. Относительная погрешность результата измерений и т. д. Относительная погрешность результата измерений
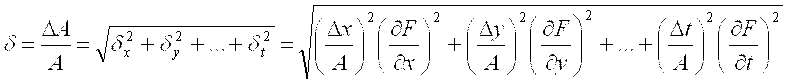 . .
Остановимся также на особенностях оценки результата косвенного измерения при наличии случайной погрешности.
Для оценки случайной погрешности результатов косвенных измерений величины А будем полагать, что систематические погрешности измерений величин x, y,…, t исключены, а случайные погрешности измерения этих же величин не зависят друг от друга.
При косвенных измерениях значение измеряемой величины находят по формуле 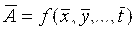 , ,
где 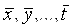 - средние или средние взвешенные значения величин x, y,…, t . - средние или средние взвешенные значения величин x, y,…, t .
Для вычисления среднего квадратического отклонения значения 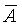 измеряемой величины А целесообразно использовать средние квадратические отклонения, полученные при измерениях x, y,…, t . измеряемой величины А целесообразно использовать средние квадратические отклонения, полученные при измерениях x, y,…, t .
В общем виде для определения среднего квадратического отклонения s косвенного измерения служит следующая формула:
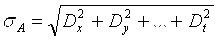 , (4.7) , (4.7)
где Dx ; Dy ;…; Dt — так называемые частные погрешности косвенного измерения 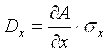 ; ;  ; …; ; …; 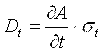 ; ; 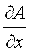 ; ; 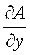 ; … ; ; … ; 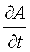 — частные производные А по x, y,…, t ; sx; sy ,…, st , …— средние квадратические отклонения результатов измерений величин x, y,…, t . — частные производные А по x, y,…, t ; sx; sy ,…, st , …— средние квадратические отклонения результатов измерений величин x, y,…, t .
Рассмотрим некоторые частные случаи применения уравнения (4.7), когда функциональная зависимость между косвенно и непосредственно измеряемыми величинами выражается формулой A = k×xa×yb×zg ,  где k - числовой коэффициент (безразмерный). где k - числовой коэффициент (безразмерный).
В этом случае формула (4.7) примет следующий вид:
 . .
Если a = b = g = 1 и A = k×x×y×z, то формула относительной погрешности упрощается до вида 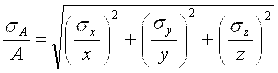 . .
Эта формула применима, например, для вычисления среднего квадратического отклонения результата измерения объема по результатам измерения высоты, ширины и глубины резервуара, имеющего форму прямоугольного параллелепипеда.
4.5. Правила суммирования случайных и систематических погрешностей
Погрешность сложных измерительных приборов зависит от погрешностей отдельных его узлов (блоков). Погрешности суммируются по определенным правилам.
Пусть, например, измерительный прибор состоит из m блоков, каждый из которых обладает независимыми друг от друга случайными погрешностями. При этом известны абсолютные значения средних квадратических sk или максимальных Мk погрешностей каждого блока.
Арифметическое суммирование  или или  дает максимальную погрешность прибора, которая имеет ничтожно малую вероятность и поэтому редко используется для оценки точности работы прибора в целом. Согласно теории ошибок результирующая погрешность sрез и Мрез определяется сложением по квадратическому закону дает максимальную погрешность прибора, которая имеет ничтожно малую вероятность и поэтому редко используется для оценки точности работы прибора в целом. Согласно теории ошибок результирующая погрешность sрез и Мрез определяется сложением по квадратическому закону  или или  . .
Аналогично определяется и результирующая относительная погрешность измерения:  . (4.8) . (4.8)
Уравнение (4.8) можно использовать для определения допустимых погрешностей отдельных блоков разрабатываемых приборов с заданной общей погрешностью измерения. При конструировании прибора обычно задаются равными погрешностями для отдельных входящих в него блоков. Если существует несколько источников погрешностей, которые на конечный результат измерения влияют неодинаково (или прибор состоит из нескольких блоков с разными погрешностями), в формулу (4.8) следует ввести весовые коэффициенты ki :
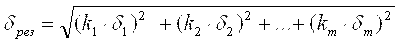 , (4.9) , (4.9)
где d1, d2, … , dm — относительные погрешности отдельных узлов (блоков) измерительного прибора; k1, k2, … , km - коэффициенты, учитывающие степень влияния случайной погрешности данного блока на результат измерения.
При наличии у измерительного прибора (или его блоков) также и систематических погрешностей общая погрешность определяется их суммой:
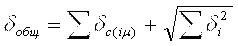 , где dс(im) - систематическая погрешность от воздейст- вия на i-й блок m-го фактора; di - случайные погрешности для i-го блока. , где dс(im) - систематическая погрешность от воздейст- вия на i-й блок m-го фактора; di - случайные погрешности для i-го блока.
Суммирование погрешностей, имеющих взаимную корреляционную связь, основано на следующем положении теории вероятностей: дисперсия суммы двух коррелированных случайных величин, характеризующихся дисперсиями 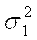 и и 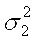 и коэффициентом корреляции r12, определяется выражением и коэффициентом корреляции r12, определяется выражением
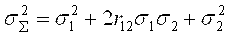 . .
Из этого следует, что средняя квадратическая результирующая погрешность вычисляется по формуле
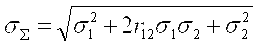 . (4.10) . (4.10)
На практике обычно пользуются двумя крайними случаями формулы (4.10); при r12 » ±1, когда составляющие погрешности суммируются алгебраически: 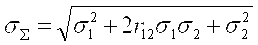 = s1+ s2 и при r12 » 0, когда погрешности суммируются геометрически: = s1+ s2 и при r12 » 0, когда погрешности суммируются геометрически: 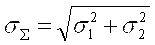 . Такой же подход справедлив и для большего числа составляющих. . Такой же подход справедлив и для большего числа составляющих.
При оценке влияния частных погрешностей следует учитывать, что точность измерений в основном зависит от погрешностей, больших по абсолютной величине, а некоторые наименьшие погрешности можно вообще не учитывать. Частная погрешность оценивается на основании так называемого критерия ничтожной погрешности, который заключается в следующем. Допустим, что суммарная погрешность dрез определена по формуле (4.8) с учетом всех m частных погрешностей, среди которых некоторая погрешность di имеет малое значение. Если суммарная погрешность d¢рез, вычисленная без учета погрешности di, отличается от dрез не более чем на 5 %, т.е. dрез-d¢рез< 0,05×dрез или 0,95×dрез<d¢рез , то di можно считать ничтожной погрешностью. Принимая во внимание, что (d¢рез)2 = d2рез - d2i , легко установить критерий ничтожной погрешности: di £ 0,3×dрез . Это означает, что если частная погрешность меньше 30 % общей погрешности, то этой частной погрешностью можно пренебречь. В случае нескольких погрешностей критерий ничтожности их совокупности имеет вид 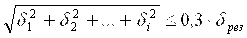 . .
В практике технических расчетов часто пользуются менее строгим критерием - в эти формулы вводят коэффициент 0,4.
4.6. Формы представления результатов измерения
Результат измерения имеет ценность лишь тогда, когда можно оценить его интервал неопределенности, т.е. степень достоверности. Поэтому результат измерений должен содержать значение измеряемой величины и характеристики точности этого значения, которыми являются систематические и случайные погрешности. Количественные показатели погрешностей, способы их выражения, а также формы представления результатов измерений регламентируются ГОСТ 8.011-72 «Показатели точности измерений и формы представления результатов измерений». Рассмотрим основные формы представления результатов измерений.
Погрешность результата прямого однократного измерения зависит от многих факторов, но в первую очередь определяется погрешностью используемых средств измерений. Поэтому в первом приближении погрешность результата измерения можно принять равной
погрешности, которой в данной точке диапазона измерений характеризуется используемое средство измерений.
Погрешности средств измерений изменяются в диапазоне измерений. Поэтому в каждом случае, для каждого измерения необходимо произвести вычисления погрешности результата измерений, используя формулы (3.19) – (3.21) нормирования погрешности соответствующего средства измерений. Вычисляться должна как абсолютная, так и относительная погрешности результата измерения, так как первая из них нужна для округления результата и его правильной записи, а вторая — для однозначной сравнительной характеристики его точности.
Для разных характеристик нормирования погрешностей СИ эти вычисления производятся по-разному, поэтому рассмотрим три характерных случая.
1. Класс прибора указан в виде одного числа q, заключенного в кружок. Тогда относительная погрешность результата (в процентах) g = q, а абсолютная его погрешность Dх = q×x/100.
2. Класс прибора указан одним числом p (без кружка). Тогда абсолютная погрешность результата измерения Dх = p×xk /100, где xk — предел измерения, на котором оно производилось, а относительная погрешность измерения (в процентах) находится по формуле 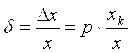 , ,
т е. в этом случае при измерении, кроме отсчета измеряемой величины х обязательно должен быть зафиксирован и предел измерений xk , иначе впоследствии нельзя будет вычислить погрешность результата.
3. Класс прибора указан двумя числами в виде c/d. В этом случае удобнее вычислить относительную погрешность d результата по формуле (3.21), а уже затем найти абсолютную погрешность как Dx = d×x/100.
После проведения вычислений погрешности используют одну из форм представления результата измерений в следующем виде: х; ±D и d, где х – измеренное значение; D – абсолютная погрешность измерения; d -относительная погрешность измерения. Например, производится следующая запись: «Измерение произведено с относительной погрешностью d = … %. Измеренное значение х = (А ± D) , где А – результат измерений».
Однако более наглядно указать пределы интервала неопределенности измеряемой величины в виде: x = (A-D)¸(A+D) или (A-D) < х < (A+D) с указанием единиц измерения.
Другая форма представления результата измерения устанавливается в следующем виде: х; D от Dн доDв; Р, где х – результат измерения в единицах измеряемой величины; D , Dн , Dв – соответственно погрешность измерения с нижней и верхней её границами в тех же единицах; Р – вероятность, с которой погрешность измерения находится в этих границах.
ГОСТ 8.011-72 допускает и другие формы представления результатов измерения, отличающиеся от приведенных форм тем, что в них указывают раздельно характеристики систематической и случайной составляющих погрешности измерения. При этом для систематической погрешности указывают её вероятностные характеристики. В этом случае основными характеристиками систематической погрешности являются математическое ожидание М[Dхс], среднеквадратическое отклонение s[Dхс] и ее доверительный интервал. Выделение систематической и случайной составляющих погрешности целесообразно, если результат измерения будет использован при дальнейшей обработке данных, например, при определении результата косвенных измерений и оценке его точности, при суммировании погрешностей и т. п.
Любая из форм представления результата измерения, предусмотренная ГОСТ 8.011-72, должна содержать необходимые данные, на основании которых может быть определен доверительный интервал для погрешности результата измерения. В общем случае доверительный интервал может быть установлен, если известны вид закона распределения погрешности и основные числовые характеристики этого закона.
.
Ваш комментарий о книге
Обратно в раздел Наука
|
|
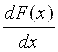 Dx или DA » ±
Dx или DA » ± 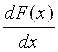 Dx.
Dx.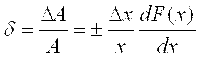 .
. .
.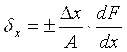 ;
; 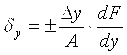 и т. д. Относительная погрешность результата измерений
и т. д. Относительная погрешность результата измерений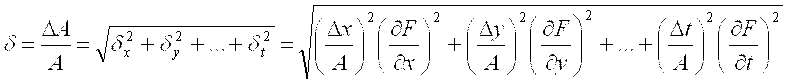 .
.![]() ,
, ![]() - средние или средние взвешенные значения величин x, y,…, t .
- средние или средние взвешенные значения величин x, y,…, t .![]() измеряемой величины А целесообразно использовать средние квадратические отклонения, полученные при измерениях x, y,…, t .
измеряемой величины А целесообразно использовать средние квадратические отклонения, полученные при измерениях x, y,…, t .![]() , (4.7)
, (4.7)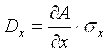 ;
;  ; …;
; …; 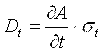 ;
; ![]() ;
; ![]() ; … ;
; … ; ![]() — частные производные А по x, y,…, t ; sx; sy ,…, st , …— средние квадратические отклонения результатов измерений величин x, y,…, t .
— частные производные А по x, y,…, t ; sx; sy ,…, st , …— средние квадратические отклонения результатов измерений величин x, y,…, t .![]() где k - числовой коэффициент (безразмерный).
где k - числовой коэффициент (безразмерный). .
. .
. или
или  дает максимальную погрешность прибора, которая имеет ничтожно малую вероятность и поэтому редко используется для оценки точности работы прибора в целом. Согласно теории ошибок результирующая погрешность sрез и Мрез определяется сложением по квадратическому закону
дает максимальную погрешность прибора, которая имеет ничтожно малую вероятность и поэтому редко используется для оценки точности работы прибора в целом. Согласно теории ошибок результирующая погрешность sрез и Мрез определяется сложением по квадратическому закону  или
или  .
. . (4.8)
. (4.8)![]() , (4.9)
, (4.9) ![]() , где dс(im) - систематическая погрешность от воздейст- вия на i-й блок m-го фактора; di - случайные погрешности для i-го блока.
, где dс(im) - систематическая погрешность от воздейст- вия на i-й блок m-го фактора; di - случайные погрешности для i-го блока.![]() и
и ![]() и коэффициентом корреляции r12, определяется выражением
и коэффициентом корреляции r12, определяется выражением ![]() .
.![]() . (4.10)
. (4.10)![]() = s1+ s2 и при r12 » 0, когда погрешности суммируются геометрически:
= s1+ s2 и при r12 » 0, когда погрешности суммируются геометрически: ![]() . Такой же подход справедлив и для большего числа составляющих.
. Такой же подход справедлив и для большего числа составляющих.![]() .
.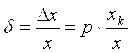 ,
,